Solution to Problem 5.8
This problem demonstrates how small changes in a program can yield dramatic performance differences, especially on a machine with out-of-order execution.
이 문제는 프로그램에서의 아주 작은 변경이 얼마나 큰 성능 차이를 만들어낼 수 있는지를 보여준다. 특히 out-of-order 실행을 지원하는 CPU에서 그 효과가 두드러진다.
Figure 5.39 diagrams the three multiplication operations for a single iteration of the function.
그림 5.39는 이 함수의 한 번의 반복(iteration) 동안 수행되는 3개의 곱셈 연산을 도식으로 보여준다.
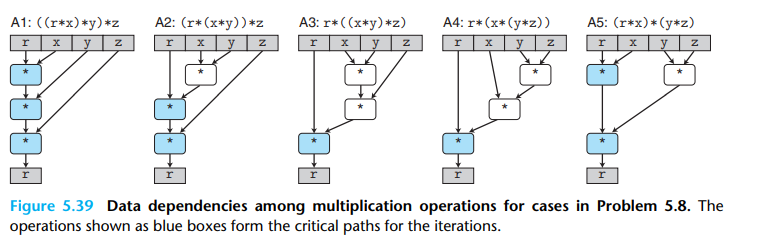
In this figure, the operations shown as blue boxes are along the critical path—they need to be computed in sequence to compute a new value for loop variable r.
이 그림에서 파란색 박스로 표시된 연산들은 임계 경로(critical path) 에 있다. 이 연산들은 루프 변수 r의 새로운 값을 계산하기 위해 반드시 순서대로 실행되어야 한다.
The operations shown as light boxes can be computed in parallel with the critical path operations.
연한 색 박스로 표시된 연산들은 임계 경로 연산들과 동시에(병렬로) 실행될 수 있다.
For a loop with P operations along the critical path, each iteration will require a minimum of 5P clock cycles and will compute the product for three elements, giving a lower bound on the CPE of 5P/3.
임계 경로에 P개의 연산이 있는 루프의 경우, 한 번의 반복을 수행하는 데 최소 5P 클록 사이클이 필요하고, 한 반복에서 3개의 원소 곱을 계산하므로, CPE의 하한(lower bound)은 5P / 3 이 된다.
This implies lower bounds of 5.00 for A1, 3.33 for A2 and A5, and 1.67 for A3 and A4.
이 계산에 따르면 CPE의 하한은 다음과 같다.
| 경우 | CPE 하한 |
| A1 | 5.00 |
| A2 | 3.33 |
| A3 | 1.67 |
| A4 | 1.67 |
| A5 | 3.33 |
We ran these functions on an Intel Core i7 Haswell processor and found that it could achieve these CPE values.
이 함수들을 Intel Core i7 Haswell 프로세서에서 실행해본 결과, 실제로 이 이론적 CPE 하한 값들에 도달할 수 있음을 확인했다.
임계 경로 : 임계 경로란, 반드시 "순서대로" 실행해야 하는 연산들의 가장 긴 의존 사슬
// 임계 경로가 긴 경우
acc = acc * a;
acc = acc * b;
acc = acc * c;
// 의존 관계
acc₀ → *a → acc₁ → *b → acc₂ → *c → acc₃
// 무조건 순서대로
// 임계 경로 길이 = 3
// 임계 경로가 짧은 경우
x = a * b;
y = c * d;
z = e * f;
acc = x * y * z;
// 의존 관계
a -> *
b -> * >> x
c -> *
d -> * >> y
e -> *
f -> * >> z
// 동시 계산
// 여기 계산은 임계 경로와 관계 없음. 굳이 순서대로 할 필요x
// acc = x * y * z 이 부분이 중요함
// CPU 내부에서는 한 번에 3개를 곱하지 못함 따라서 이렇게 계산이 됨
t = x * y;
acc = t * z;
// 곱셈 2번. 둘다 순서대로 실행해야 한다.
// 임계 경로의 길이는 여기서 사용한 곱셈의 갯수로 정해짐
// 따라서 임계 경로는 2이다
CPE : 원소 하나를 처리하는 데 평균적으로 걸리는 CPU 사이클의 수
(CPU = 총 CPU 사이클 수 / 처리한 원소의 개수)
CPE ≥ (실수 곱셈 × 임계 경로 상의 곱셈의 개수) ÷ 한번에 처리 가능한 원소의 수
CPE ≥ (5 × 2) ÷ 3 = 3.33
CPE의 하한 : 어떤 최적화를 해도 절대로 내려갈 수 없는 최소 CPE
'컴퓨터과학(CS) > CS문제 풀이' 카테고리의 다른 글
| Solution to Problem 5.10 (0) | 2026.01.18 |
|---|---|
| Solution to Problem 5.9 (0) | 2026.01.18 |
| Solution to Problem 5.7 (0) | 2026.01.18 |
| Solution to Problem 4.39 ~ 4.44 (1) | 2026.01.08 |
| 어셈블리 명령어 단계별 실행 분석 – Problem 4.14 (0) | 2025.12.28 |

